Hüsnü Ata Erbay’ın araştırmaları genel olarak Uygulamalı Matematik alanında olup, üç ana gruba ayrılabilir. Bunlardan birincisi, fizik ve mühendislikte ortaya çıkan çeşitli olayların diferansiyel denklemlerle ifade edilebilen matematiksel modellerinin inşa edilmesidir. İkincisi ise, bu modellerin matematiksel analizinin gerçekleştirilmesi, yani bu modeller yardımıyla tanımlanan matematiksel problemlerin çözümlerinin varlığı, tekliği, kararlılığı, asimptotik davranışı ve zaman içerisinde tekilliklere dönüşmesi gibi niteliksel özelliklerinin araştırılmasıdır. Üçüncü grup; tanımlanmış matematiksel problemlerin kesin veya yaklaşık çözümlerinin elde edilebilmesi için gerçekleştirilen bilimsel çalışmalardır. Her üç grupta halen yürütülen araştırmaların en önemli ortak özelliği doğrusal olmama (nonlineerlik) olarak ifade edilebilir. Bu bağlamda; doğrusal yaklaşımlarla ifade edilemeyen olayların doğrusal olmayan matematiksel modellerinin inşa edilmesi, bu modellerin matematiksel analizi ve çözümlerinin incelenmesi halen yürütülmekte olan araştırmaların temel çerçevesi olarak belirtilebilir.
Hüsnü Ata Erbay’ın çalışma arkadaşları ile birlikte son zamanlarda yürüttüğü araştırmalarda; elastik malzemeden oluşan sürekli ortamlar için literatürde önerilmiş yerel olmayan elastisite ve peridinamik elastisite kuramları çerçevesindeki doğrusal olmayan matematiksel modeller önemli bir yer tutmaktadır. Doğrusal olmama özelliğine ek olarak, sözkonusu modellerin farklı fiziksel etkileri karakterize eden farklı ölçekleri de birarada içermesi bu çok ölçekli matematiksel modelleri hem modelleme hem de matematiksel analiz açısından oldukça karmaşık bir hale getirmektedir. Bu karmaşıklık; ele alınan matematiksel problemlerin çözümlerinin varlığı, tekliği, kararlılığı, asimptotik davranışı, zaman içerisinde tekilliklere dönüşmesi, gezen dalga çözümleri ve onların yörüngesel kararlılığı gibi en temel soruları cevaplayabilmek için yeni matematiksel teknikler geliştirmeyi gerektirir.
Doğrusal olmayan matematiksel modellerle ifade edilen problemlere, genellikle, sadece çok özel durumlarda kesin çözümler bulunabilmektedir. Bu durumda, modelle ilgili çeşitli sorulara en azından kısmi/yaklaşık cevaplar verilebilmesini sağlamak için, çok sayıda matematikçi sayısal teknikler geliştirerek yaklaşık çözümler elde etmeye çalışmaktadır. Bu yaklaşımların, özellikle, yalnız dalgaların (solitary waves) doğrusal olmayan yayılımını karakterize eden doğrusal olmayan diferansiyel denklemlere genişletilmesi Hüsnü Ata Erbay ve çalışma arkadaşlarının son zamanlarda yürüttüğü araştırmaların bir diğer konusunu oluşturmaktadır. Sonlu farklar (finite-differences) ve bölünmüş adım (split-step) sayısal çözüm yöntemleri bu araştırmalarda en çok kullanılmış sayısal yöntemlerdir. Aşağıda iki örnek probleme ait sayısal deney sonuçları verilmiştir.
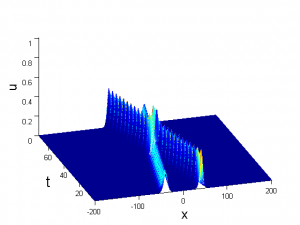
İlk örnek; farklı genliklere ve farklı hızlara sahip birbirlerine doğru ilerleyen iki yalnız dalganın çarpışmasına aittir. Bu dalgaların yayılımını yöneten doğrusal olmayan dalga denkleminin bir sayısal yöntemle çözümünden elde edilmiş sayısal sonuçlar; x konum, t zaman ve u(x,t) bağımlı değişken olmak üzere aşağıdaki şekilde sunulmaktadır. Hem büyük genlikli ve hem de küçük genlikli dalgaların çarpışmadan sonra da özelliklerini koruduğu gözlenmektedir. Bu gözlem ile doğrusal olmama arasındaki bağıntı bir araştırma konusudur.
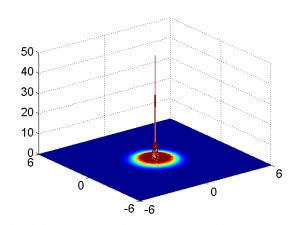
Doğrusal olmayan diferansiyel denklemlerle tanımlanmış matematiksel problemlerin hiç bir çözümlerinin mevcut olmadığı örnekler olduğu gibi, mevcut bir düzgün çözümünün zaman içersinde bir tekilliğe dönüştüğü örnekler de vardır. Aşağıdaki şekilde; doğrusal olmayan bir dalga denkleminin sayısal yöntemlerle çözümünden elde edilmiş ve birim genlikli düzgün bir başlangıç datasının sonlu zamanda bir tekilliğe dönüşmesine ait sayısal sonuçlar sunulmaktadır. Burada yatay eksenler x ve y konumlarını, düşey eksen u(x,y,t) bağımlı değişkenini göstermekte olup, şekilde belirli bir t zamanı için u büyüklüğünün uzaysal değişimi verilmektedir. Çözümün sözkonusu zamandaki genliğinin başlangıç datası genliğinin yaklaşık 50 katına ulaştığı gözlenmektedir. Doğrusal olmama ile bu gözlem arasındaki bağınti yine bir araştırma konusudur.